题目内容
（请给出正确答案）
[主观题]
设σ是数域F上n维向量空间V的一个可以对角化的线性变换。令λ1，λ2，···，λt是σ的全部本
征值。证明，存在V的线性变换σ1，σ2，···，σt，使得
查看答案
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
更多“设σ是数域F上n维向量空间V的一个可以对角化的线性变换。令λ…”相关的问题
设V是数域F上一切mxn矩阵所构成的向量空间。C是一个取定的mxm矩阵，定义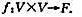
证明：f是V上一个双线性函数，f是不是对称的？
设V和W都是数域F上的向量空间，且dimV=n。令σ是V到W的一个线性映射。我们如此选取V的一个基：α1，···，αs，αs+1，...，αn，使得α1，···，αs是Ker(σ)的一个基。证明：(i)σ(αs+1)，...，σ(αn)组成Im(σ)的一个基；
(ii)dim Ker(σ)+dim Im(σ)=n。
设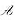
是数域P上n维线性空间V的一个线性变换，证明：
1)在P[x]中有一次数≤n2的多项式f(x)，使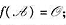
2)如果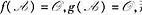
，那么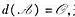
这里d(x)是f(x)与g(x)的最大公因式;
3)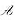可逆的充分必要条件是，有一常数项不为零的多项式f(x)使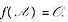
设{α1，α2，···，αn}是F上n维向量空间V的一个基。A是F上一个nxs矩阵。令
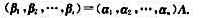证明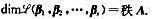
令Mn(F)表示数域F上一切n阶矩阵所组成的向量空间。令
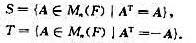
证明：S和T都是Mn(F)的子空间，并且Mn(F)=S+T，S∩T={O}。
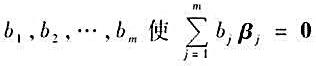。则或者b1=b2=...=bm=0，或者b1，b2，...，bm皆不为零。在后者的情形，若有另一组数c1，c2，...，cm使
。
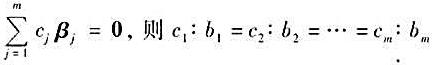