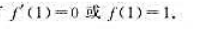题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
[主观题]
设P(x)是n次多项式函数.证明:1)若P(a),P’(a)...P(n)(a)都是正数,则P(x)在(a,+∞)无零点;2)若P(a),P’(a)...P(n)(a)正负号相间,则P(x)在(-∞,a)无零点.
设P(x)是n次多项式函数.证明:1)若P(a),P’(a)...P(n)(a)都是正数,则P(x)在(a,+∞)无零点;2)若P(a),P’(a)...P(n)(a)正负号相间,则P(x)在(-∞,a)无零点.
查看答案
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案


 更多“设P(x)是n次多项式函数.证明:1)若P(a),P’(a)…”相关的问题
更多“设P(x)是n次多项式函数.证明:1)若P(a),P’(a)…”相关的问题
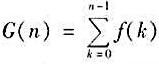 对所有n≥1成立的充分必要条件是G(x+1)-G(x)=f(x)且G(0)=0;
对所有n≥1成立的充分必要条件是G(x+1)-G(x)=f(x)且G(0)=0;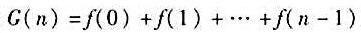 对任何n≥1的整数成立;
对任何n≥1的整数成立;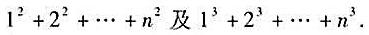
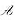 是数域P上n维线性空间V的一个线性变换,证明:
是数域P上n维线性空间V的一个线性变换,证明: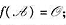
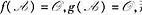 ,那么
,那么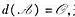 这里d(x)是f(x)与g(x)的最大公因式;
这里d(x)是f(x)与g(x)的最大公因式;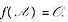
 的次数分别为n1,n2,...,ns。证明:若
的次数分别为n1,n2,...,ns。证明:若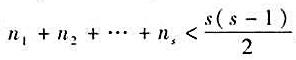 ,则
,则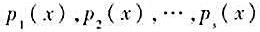 在线性空间P[x]中线性相关。
在线性空间P[x]中线性相关。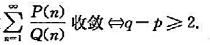
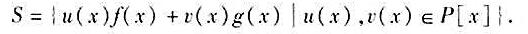
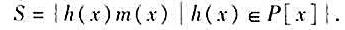
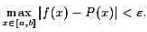 其中ε是预先给定的任意正数.
其中ε是预先给定的任意正数.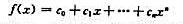 。用线性方程组的理论证明,若f(x)有n+1个不同的根,那么f(x)是零多项式。
。用线性方程组的理论证明,若f(x)有n+1个不同的根,那么f(x)是零多项式。