 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
设A是全体正实数所成的集合,令(i)g是不是A到A的双射?(ii)g是不是f的逆映射?(iii)如果g有逆映射
设A是全体正实数所成的集合,令
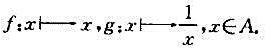
(i)g是不是A到A的双射?
(ii)g是不是f的逆映射?
(iii)如果g有逆映射,g的逆映射是什么?
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
设A是全体正实数所成的集合,令
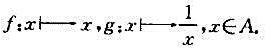
(i)g是不是A到A的双射?
(ii)g是不是f的逆映射?
(iii)如果g有逆映射,g的逆映射是什么?
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 更多“设A是全体正实数所成的集合,令(i)g是不是A到A的双射?(…”相关的问题
更多“设A是全体正实数所成的集合,令(i)g是不是A到A的双射?(…”相关的问题
设G是一个群,a∈G。映射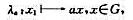 叫做G的一个左平移。证明:
叫做G的一个左平移。证明:
(i)左平移是G到自身的一个双射;
(ii)设a,b∈G,定义λaλb=λa·λb(映射的合成),则G的全体左平移{λa|a∈G}对于这样定义的乘法作成一个群G';
(iii)G≌G'。
设G={a,b,c,d},其中
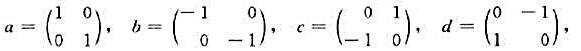
G上的运算是矩阵乘法。
(1)找出G的全部子群。
(2)在同构的意义下G是4阶循环群还是Klein四元群?
(3)令S是G的所有子群的集合,定义S上的包含关系 ,则<S,
,则<S, >构成偏序集,画出这个偏序集的哈斯图。
>构成偏序集,画出这个偏序集的哈斯图。
设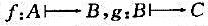 是映射,又令
是映射,又令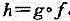 ,证明:
,证明:
(i)如果h是单射,那么f也是单射;
(ii)如果h是满射,那么g也是满射;
(iii)如果f,g都是双射,那么h也是双射,并且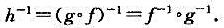
设 R[t]为t的实系数多项式的集合,![设 R[t]为t的实系数多项式的集合,为t的n次实系数多项式的集合.定义函数f:R[t]→R[t],](https://img2.soutiyun.com/ask/2021-02-23/982943323474961.png) 为t的n次实系数多项式的集合.定义函数f:R[t]→R[t],f(g(t))=g2(t).求f(R0[1]).f-1({t2+2t+1}).f-1(f({t-1,t2-1})).
为t的n次实系数多项式的集合.定义函数f:R[t]→R[t],f(g(t))=g2(t).求f(R0[1]).f-1({t2+2t+1}).f-1(f({t-1,t2-1})).
问题描述:给定有向图G=(V,E).设P是G的一个简单路(顶点不相交)的集合.如果V中每个顶点恰好在P的条路上,则称P是G的一个路径覆盖.P中路径可以从V的任何一个项点开始,长度也是任意的,特别地,可以为0.G的最小路径覆盖是G的所含路径条数最少的路径覆盖.
设计一个有效算法求一个有向无环图G的最小路径覆盖.
[设V={1,2,...,n},如下构造网络G1=(V1,E1):
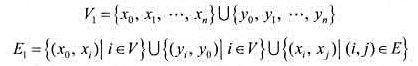
每条边的容量均为1.求网络G1的(x0,y0)最大流.]
算法设计:对于给定的有向无环图G,找出G的一个最小路径覆盖.
数据输入:由文件input.txt提供输入数据.文件第1行有2个正整数n和m.n是给定有向无环图G的顶点数,m是G的边数.接下来的m行,每行有2个正整数i和j,表示一条有向边(i,j).
结果输出:将最小路径覆盖输出到文件output.txt.从第1行开始,每行输出一条路径.文件的最后一行是最少路径数.

设


证明:(1) 若E是闭集,
(2) 若

A.壬申之乱
B.承久之乱
C.建武新政
D.应仁·文明之乱2讲