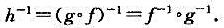题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
[主观题]
设G是一个群,a∈G。映射叫做G的一个左平移。证明:(i)左平移是G到自身的一个双射;(ii)设a,b∈G,定义
设G是一个群,a∈G。映射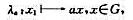 叫做G的一个左平移。证明:
叫做G的一个左平移。证明:
(i)左平移是G到自身的一个双射;
(ii)设a,b∈G,定义λaλb=λa·λb(映射的合成),则G的全体左平移{λa|a∈G}对于这样定义的乘法作成一个群G';
(iii)G≌G'。
查看答案
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案


 更多“设G是一个群,a∈G。映射叫做G的一个左平移。证明:(i)左…”相关的问题
更多“设G是一个群,a∈G。映射叫做G的一个左平移。证明:(i)左…”相关的问题
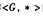 是一个群,H,K是其子群.定义G上的关系R:对任意a,b
是一个群,H,K是其子群.定义G上的关系R:对任意a,b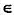 G,aRb
G,aRb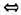 存在h
存在h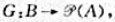 对于b∈B,有
对于b∈B,有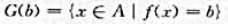 证明:如果f是A到B的满映射,则G是入射的,其逆成立吗?
证明:如果f是A到B的满映射,则G是入射的,其逆成立吗?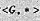 为一个群.证明:
为一个群.证明: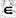 G有a2=e,则G为阿贝尔群.
G有a2=e,则G为阿贝尔群.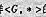 为群,a为G中阶为k的元素,集合
为群,a为G中阶为k的元素,集合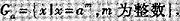
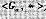 是否构成一个群,为什么?
是否构成一个群,为什么?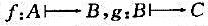 是映射,又令
是映射,又令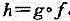 ,证明:
,证明: