 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
设{α1,α2,···,αn}是F上n维向量空间V的一个基。A是F上一个nxs矩阵。令证明
设{α1,α2,···,αn}是F上n维向量空间V的一个基。A是F上一个nxs矩阵。令
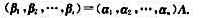 证明
证明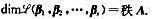
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
设{α1,α2,···,αn}是F上n维向量空间V的一个基。A是F上一个nxs矩阵。令
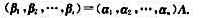 证明
证明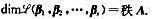
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 更多“设{α1,α2,···,αn}是F上n维向量空间V的一个基。…”相关的问题
更多“设{α1,α2,···,αn}是F上n维向量空间V的一个基。…”相关的问题
设![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978874955275302.png) 是数域P上n维线性空间V的一个线性变换,证明:
是数域P上n维线性空间V的一个线性变换,证明:
1)在P[x]中有一次数≤n2的多项式f(x),使![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978874992094408.png)
2)如果![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978875015617754.png) ,那么
,那么![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978875034333824.png) 这里d(x)是f(x)与g(x)的最大公因式;
这里d(x)是f(x)与g(x)的最大公因式;
3)![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978874955275302.png) 可逆的充分必要条件是,有一常数项不为零的多项式f(x)使
可逆的充分必要条件是,有一常数项不为零的多项式f(x)使![设是数域P上n维线性空间V的一个线性变换,证明:1)在P[x]中有一次数≤n2的多项式f(x),使2](https://img2.soutiyun.com/ask/2021-01-07/978875092573155.png)
给定方程组x'(t)=A(t)x(t), ①
这里A(t)是[a,b]上的连续n×n,函数矩阵。设Φ(t)是①的一个基解矩阵,n维向量函数F(t,x)在R:a≤t≤b,‖x‖<∞上连续,t0∈[a,b]。试证明:初值问题
![给定方程组x'(t)=A(t)x(t), ① 这里A(t)是[a,b]上的连续n×n,函](https://img2.soutiyun.com/latex/latex.action)
的唯一解ψ(t)是积分方程组
x(t)=Φ(t)Φ-1(t0)η+∫t0tΦ(t)Φ-1(s)F(s,x(s))ds ②
的连续解。反之,②的解也是初值问题②的解。
F是一个数域,A是F上的n阶方阵,集合W={B∈Fn*n|AB=0} 证明:(1)w是Fn*n的子空间 (2)若A的秩为R,求W的维数
设V是复数域上的n维线性空间,T1,T2是V上的线性变换,且T1T2=T2,T1,证明: (1)如果λ0是T1的特征值,则Vλ0是T2的不变子空间; (2)T1,T2至少有一个公共的特征向量.
设A是复数域C上一个n阶矩阵,λ1,λ2,···,λn是A的全部特征根(重根按重数计算)。
(i)如果f(x)是C上任意一个次数大于零的多项式,那么f(λ1),f(λ2),···,f(λn)是f(A)的全部特征根;
(ii)如果A可逆,那么λi≠0,i=1,2,...,n,并且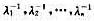 是A-1的全部特征根。
是A-1的全部特征根。
设A(t),f(t)分别为在区间a≤t≤b上连续的n×n矩阵和n维列向量,f(t)≠0. 证明方程组
x'=A(t)x+f(t) (*)
存在且最多存在n+1个线性无关解。
设α1,α2,···,αn是n维欧氏空向Rn的一组基。证明:
(1)若γ∈Rn,有(γ,αi)=0,i=1,2,...,n,则γ是零向量;
(2)若γ1,γ2∈Rn,使对Rn中任意向量α,均有<γ1,α>=<γ2,α>,那么γ1=γ2。